Quando il caos è più complicato di quanto si pensi
Una delle speranze dei filosofi naturali fino alla fine dell’Ottocento era quella di poter usare leggi deterministiche per descrivere tutti i fenomeni meccanici. Date posizioni e velocità di ogni oggetto dell’universo con una certa precisione, sarebbe stato possibile conoscere il futuro e il passato. Ma a cavallo tra il XIX e il XX secolo Henri Poincaré dimostrò la presenza del caos: quando il passato determina il futuro, ma un’approssimazione del passato non determina approssimativamente il futuro. Due stati iniziali senza apprezzabile differenza evolvono lungo strade completamente diverse, e incidentalmente non è possibile ritornare indietro nel tempo e risalire alla configurazione iniziale che ha portato a quella corrente.
Quando Poincaré aveva incontrato il caos, lui stesso aveva in qualche modo gettato la spugna, affermando, in riferimento alla figura che aveva in mente per descriverlo, che «si sarà colpiti dalla complessità di tale figura, che non tento nemmeno di tracciare». Come abbiamo visto nella terza uscita della nostra rivista, si trattava delle infinite e sempre più fitte intersezioni di due insiemi, uno lungo il quale la dinamica in qualche senso “contrae” o “accorcia” l’evoluzione del sistema (varietà stabile) e uno lungo il quale la dinamica le “stira” o “allunga” (varietà instabile). In qualche modo, il caos emerge naturalmente ogni volta che un sistema dinamico presenta contemporaneamente due evoluzioni, una che allunga e un’altra che accorcia, ciascuna lungo due “direzioni” trasversali l’una rispetto all’altra, e si parla in questo caso di un sistema iperbolico. Il matematico francese arrivò a queste conclusioni mentre si occupava del moto dei pianeti, anzi di un caso estremamente semplificato: la sua scoperta era significativa perché mostrava che anche un semplice sistema dinamico deterministico, non necessariamente un complicatissimo insieme di un numero di Avogadro di molecole, poteva produrre una dinamica imprevedibile. Eppure, per decenni a venire, astronomi, fisici e matematici del caos non si occuparono.

Figura 1. Alcune intersezioni della varietà stabile (tratto fine) e della varietà instabile (tratto spesso), le due curve che si ripiegano l’una sull’altra, come immaginato da Poincaré.
Finché, nella prima metà degli anni Sessanta, qualcuno non fu in qualche modo obbligato ad aprire gli occhi. Con l’arrivo dei calcolatori (leggi: computer), era finalmente possibile simulare con poche righe di codice un sistema dinamico descritto da qualche astratta equazione, e farsi stampare graficamente su schermo la sua evoluzione in modo da capirci qualcosa. Ad esempio, grazie al calcolatore posso abbozzare la complicata figura immaginata da Poincaré (Figura 1). Ebbene, quando i fisici matematici (Contopoulos, Hénon e Heiles, solo per citarne alcuni) cominciarono a farsi stampare queste mappe dinamiche di sistemi anche relativamente semplici, si trovarono davanti agli occhi figure stravaganti. Alcune orbite, ovvero evoluzioni del sistema dinamico a partire da un certo dato iniziale, erano perfettamente ordinate e regolari, ma allo stesso tempo vi erano orbite che facevano di tutto e di più, coprendo zone intere dello schermo di punti che andavano da tutte le parti (Figura 2). A qualcuno venne in mente che potessero essere proprio le figure che Poincaré aveva predetto. Era la riscoperta, sessant’anni dopo, della coesistenza dell’ordine e del caos nei sistemi dinamici.

Figura 2. Esempio di coesistenza di ordine (le “isole” tonde dove la dinamica rimane confinata a girare e tornare sempre sui suoi passi) e caos (le aree riempite disordinatamente di punti, generati con diversi dati iniziali).
Ma ai lettori più attenti sarà certamente sorto un dubbio per nulla banale: se è vero che anche un sistema dinamico semplice può essere caotico, come posso sperare di seguire fedelmente una mappa dinamica usando un computer, che soffre del serio problema di non avere un’infinita precisione di calcolo ed è perciò necessariamente soggetto a errori di troncamento? Quando provo a calcolare un’orbita, a ogni passo compio un errore numerico, che si propaga caoticamente nelle evoluzioni successive, anch’esse affette dai loro errori di troncamento… insomma, sembra che io debba buttare tutto nel cestino. Per fortuna, esiste un bellissimo risultato che ci salva quando tutto sembra perduto.
Cominciamo a dare qualche definizione. Abbiamo detto che, dato un sistema dinamico[1], una sua orbita è una sequenza di punti ottenuta a partire da un qualche punto iniziale, e ciascun altro punto è ottenuto a partire dal precedente seguendo l’evoluzione del sistema passo passo. Ma abbiamo anche detto che un computer non è in grado di calcolare con infinita precisione una tale evoluzione a causa di errori di troncamento: quello che il computer calcola per ogni dato punto iniziale è una epsilon-orbita, ovvero una sequenza di punti in cui ciascuno è ottenuto a partire dal precedente seguendo l’evoluzione del sistema ma commettendo a ogni passo un errore di al più ε, dove possiamo sperare che ε > 0 sia un numero piccolo. Ad esempio, si potrebbe dire che una vera orbita è una 0-orbita, tale cioè per cui a ogni passo l’errore commesso è zero. Ma il computer può calcolare solo ε-orbite con ε strettamente maggiore di zero: supponiamo di averne calcolata una e chiamiamola P. Sarebbe fantastico se esistesse un’altra vera orbita Q (non necessariamente una con lo stesso dato iniziale, ma comunque un’autentica orbita) che segue P durante tutta la dinamica, in maniera tale che ogni punto dell’evoluzione di Q rimane vicino al corrispettivo punto della ε-orbita P, come facendogli da ombra. Diciamo ad esempio che non ne sia distante più di una certa quantità δ > 0, che di nuovo possiamo sperare piccola (Figura 3). In questo modo, potremmo sentirci rassicurati e dire che la nostra ε-orbita, piena di errori di calcolo dovuti a troncamenti, non è poi da buttare, perché ciascun punto rimane comunque una buona approssimazione di un punto di un’orbita che ha tutto il diritto di essere chiamata tale. Chiamiamo una vera orbita del sistema dinamico una δ-orbita ombra della nostra data ε-orbita se, a ogni passo, i corrispondenti punti della ε-orbita e di tale vera orbita non distano più di δ uno dall’altro. Ebbene, nel caso di sistemi iperbolici (cioè come abbiamo detto sistemi in cui vi è una direzione che contrae e una direzione che allunga), il lemma dell’orbita ombra afferma che queste δ-orbite ombra esistono eccome. Per la precisione, il lemma afferma che, per ogni δ > 0 (ovvero, per ogni “livello massimo di ombreggiamento” scelto a piacere) esiste un ε > 0 (ovvero, un “livello massimo di errore nel calcolo dell’orbita”) tale che ogni ε-orbita ammette una δ-orbita ombra.
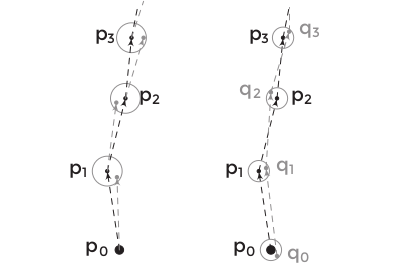
Figura 3. A sinistra, una ε-orbita P={p₀, p₁, p₂, p₃,…} (i punti in nero) generata a partire dal dato iniziale p₀: a ogni passo, la vera dinamica sarebbe quella mostrata dalla freccia grigia e ci porterebbe al punto grigio, ma viene commesso un errore e si raggiunge un altro punto, quello nero; i cerchi grigi sono di raggio costante ε e mostrano come i corrispettivi punti nero e grigio distano meno di ε l’uno dall’altro. A destra, la stessa ε-orbita (in nero) e una sua δ-orbita ombra Q={q₀, q₁, q₂, q₃,…} (in grigio): quest’ultima è un’autentica orbita della dinamica con la proprietà che a ogni passo i corrispettivi punti nero e grigio distano meno di δ l’uno dall’altro (come mostrano i cerchi grigi, di raggio costante δ).
Se sono riuscito a spiegarmi con sufficientemente chiarezza, questo risultato dovrebbe colpire il lettore ancora di più di quanto potesse sperare Poincaré: in un sistema caotico, che di nuovo significa intuitivamente un sistema in cui due orbite anche partendo infinitesimamente vicine se ne vanno per i fatti loro, è comunque possibile prendere un’orbita calcolata a ogni passo solo approssimativamente e attaccarci di fianco un’autentica orbita in modo tale che le due rimangano vicine una all’altra lungo l’intera evoluzione! E se anche non sono riuscito a spiegarmi e ho fatto solo confusione va bene lo stesso: si sarà almeno capito che il caos è più complicato di quanto non si possa immaginare.
Note
[1] Per la precisione, stiamo parlando di mappe discrete e non continue, un po’ come un film è una successione di un numero finito di istantanee che fotografano un processo che in realtà si svolge continuamente in ogni istante di tempo. D’altra parte questa è un’altra limitazione del digitale.




